If you’ve ever written code in Python, CUDA, or TensorFlow, you’ve probably seen terms like float16, float32, or float64. They map directly to the IEEE-754 floating-point standard:
- Half precision (16 bits)
- Single precision (32 bits)
- Double precision (64 bits)
But what do these formats really mean? Why does 16-bit give you only “3 digits of accuracy,” and why is 32-bit called single precision while 64-bit is double? Let’s dive in — and also tackle the common confusions people face when they first see binary scientific notation.
The Core Idea: Scientific Notation in Binary
In decimal, we write large or small numbers in scientific notation: 6.022×10236.022 \times 10^{23}
- 6.022 → significant digits
- 10²³ → scaling factor
Floating point does exactly the same thing in binary:
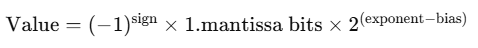
- Sign → 1 bit for +/−
- Exponent → controls scale (powers of 2)
- Mantissa (fraction/significand) → stores the significant digits
Example: Representing the Number 5
- Decimal 5 = binary 101₂.
Now we want to write this like binary scientific notation. Move the “binary point” until only one digit remains before it:
101₂ = 1.01₂ × 2²
At first glance, someone might think:
“But 1.01 × 4 = 4.04, not 5!”
That’s the classic confusion.
Here’s the fix:
1.01₂is not decimal 1.01.- It means 1+0/2+1/4=1.251 + 0/2 + 1/4 = 1.25 in decimal.
- So:
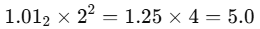
✅ Exactly right.
Binary Fractions Cheat Sheet
To avoid tripping over this:
| Binary fraction | Decimal value |
|---|---|
| 0.1₂ | 0.5 |
| 0.01₂ | 0.25 |
| 0.11₂ | 0.75 |
| 1.01₂ | 1.25 |
So whenever you see a binary point, think in terms of powers of 2 (½, ¼, ⅛…), not powers of 10.
Precision: Why Half = ~3 Digits, Single = ~7, Double = ~16
The mantissa is where precision lives. Each mantissa bit lets you store one more “digit” in binary. To estimate decimal precision, we convert bits → digits:
decimal digits≈mantissa bits×log10(2)
Since log10(2)≈0.301:
- Half precision (10 mantissa bits + 1 hidden):
1×0.301≈3.3 → ~3 digits - Single precision (23 + 1 = 24 bits):
24×0.301≈7.2 → ~7 digits - Double precision (52 + 1 = 53 bits):
53×0.301≈15.95 → ~16 digits
So if you store π (3.14159…):
- Half → 3.14
- Single → 3.141593
- Double → 3.141592653589793
Why “Half,” “Single,” and “Double”?
Historically, 32-bit was the standard float size on most hardware — called single precision. Then:
- Half precision (16-bit) is literally half of single.
- Double precision (64-bit) is twice single.
Why Does It Look So Weird?
This scheme was designed in the early 1980s by the IEEE 754 committee, led by mathematician William Kahan (“the father of floating point”). Their goals:
- Wide range & predictable accuracy
- Efficient hardware implementation
- Consistency across platforms
Before this, every vendor had their own floating-point rules, which made numerical code unpredictable. IEEE-754 unified the world.
Takeaways
- Floating point = scientific notation in binary.
- Mantissa = significant digits, controls accuracy.
- Exponent = scale, controls size range.
- Half, single, double differ only in how many bits they allocate.
👉 That’s why:
- Half precision = ~3 decimal digits
- Single precision = ~7 decimal digits
- Double precision = ~16 decimal digits
Floating-point formats may look strange at the bit level, but they’re nothing more than binary scientific notation with fixed storage budgets. Once you understand the split between exponent (scale) and mantissa (precision), the whole system makes sense: half precision gives you about 3 reliable digits, single precision about 7, and double precision about 16. Whether you’re tuning a deep learning model, running a simulation, or just curious why your decimal “5” becomes 1.01₂ × 2², this knowledge helps you reason about when numbers are trustworthy and when they’re not. In short: floating point isn’t magic — it’s carefully engineered compromise.
