LoRA: Low-Rank Adaptation Made Simple

Large language models are huge — billions of parameters, often stored as massive square weight matrices like 4096 × 4096. Fine-tuning all of those parameters for a new task is expensive, slow, and memory-hungry.

LoRA (Low-Rank Adaptation) offers a clever shortcut: instead of adjusting every cell in those giant matrices, it learns structured low-rank updates that are small, efficient, and surprisingly powerful.

1. Foundations

1.1 Standard Linear Layer

A normal linear layer looks like:

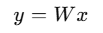
where W is a big weight matrix (e.g. 4096 × 4096 = ~17M parameters).

1.2 Adding LoRA Updates

With LoRA, we freeze W and add a trainable update:

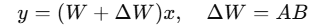
• A: (4096×r)
• B: (r×4096)
• r: the rank (small number, e.g. 8 or 16)

This reduces the number of training parameters from millions to just tens of thousands.

2. Understanding Rank

2.1 Rank in Linear Algebra

• For any m×n matrix: rank(M)≤min(m,n)
• Examples:
  • A 100 × 200 matrix → max rank = 100
  • A 200 × 100 matrix → max rank = 100
  • A 4096 × 4096 matrix → max rank = 4096

2.2 Rank in LoRA

• Rank defines the number of independent directions of change allowed.
• LoRA with r=8 means 8 “master knobs” control the update.
• ΔW=AB still expands into a full 4096 × 4096 matrix, so every cell can change — but only in structured ways.

👉 Essence: rank limits how weights can move, not where.

3. Practical Considerations

3.1 Choosing the Rank

Rank is a hyperparameter chosen by you:

• Small r (4–8): efficient, tiny adapters, less expressive
• Larger r (32–64+): closer to full fine-tuning, more resource cost

Typical defaults:

• LLaMA-7B → r=8 or 16
• Larger models or complex tasks → r=32+

3.2 Why LoRA Works

Neural nets are over-parameterized. Restricting updates to a low-rank subspace is often enough to reprogram them for a new task, while saving memory and compute.

4. Implementation in Practice

4.1 Libraries

The standard Python library for LoRA is PEFT (Hugging Face).

4.2 Example Code

from transformers import AutoModelForCausalLM, AutoTokenizer, TrainingArguments
from peft import LoraConfig, get_peft_model

# Load base model
model_name = "meta-llama/Llama-2-7b-hf"
model = AutoModelForCausalLM.from_pretrained(model_name)
tokenizer = AutoTokenizer.from_pretrained(model_name)

# Configure LoRA
lora_config = LoraConfig(
    r=8,
    lora_alpha=16,
    target_modules=["q_proj", "v_proj"],
    lora_dropout=0.05,
    bias="none",
    task_type="CAUSAL_LM"
)

# Apply LoRA
model = get_peft_model(model, lora_config)

# Training args (simplified example)
training_args = TrainingArguments(
    per_device_train_batch_size=2,
    num_train_epochs=3,
    learning_rate=2e-4,
    output_dir="./lora-out"
)

5. Outputs and Checkpoints

5.1 Default Output

LoRA training produces adapter weights only (A and B).

• Small files (MBs instead of GBs)
• Must be loaded alongside the frozen base model

5.2 Merging into Standalone Model

If you want a single full checkpoint:

from peft import PeftModel

model = AutoModelForCausalLM.from_pretrained(model_name)
model = PeftModel.from_pretrained(model, "./lora-out")

# Merge
model = model.merge_and_unload()
model.save_pretrained("./merged-model")

Now ./merged-model behaves like a normal fine-tuned model — no adapter files required.

6. Takeaways

• LoRA adapters are low-rank modules injected into existing layers.
• Rank r = how many independent update directions are allowed.
• LoRA is efficient: small adapters + option to merge into full checkpoint.
• It works because LLMs are highly redundant — small structured updates go a long way.

👉 LoRA gives you fine-tuning power at a fraction of the cost.